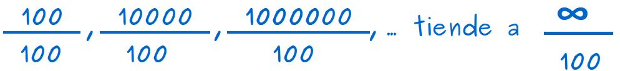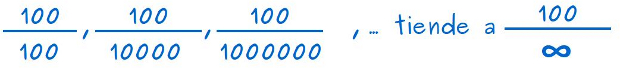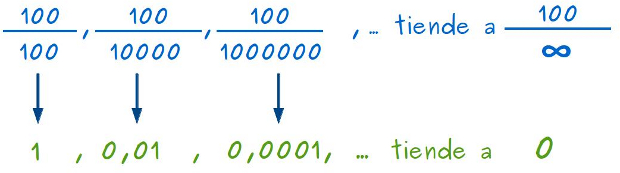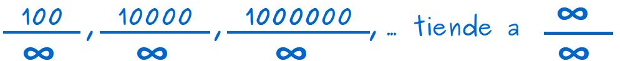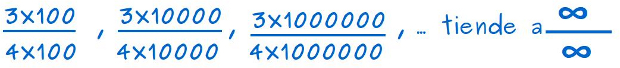http://cuidadoconloshuevos.blogspot.com/2011/12/medidas-economicas-rajoy-exclusiva.html
¿PORQUÉ ESPAÑA ODIA LA CIENCIA?
10 COSAS SOBRE FISICA GENERAL QUE HASTA BELEN ESTEBAN DEBERIA SABER
Ilusión visual: el tejado que desafía la gravedad
Kokichi Sugihara vuelve a jugar con nuestra percepción con su último trabajo.
Hablamos con el matemático japonés que da vida a los objetos de M.C. Escher.
La última ilusión visual de Kokichi Sugihara fue presentada hace unos días en la Conferencia Europea de Percepción Visual en Alguer, en la isla de Cerdeña. En la imagen observamos un tejado sobre el que caen unas bolas, pero nada es lo que parece. Como en anteriores ocasiones, sus geometrías recuerdan a los dibujos de M.C. Escher y sus juegos con la percepción espacial.Sugihara es profesor en la universidad de Meiji, en Kawasaki, Japón, y uno de sus trabajos fue nombrado «la ilusión visual del año 2010». Sus ilusiones son el resultado de la investigación con un programa para que los ordenadores diferencien objetos reales e interpreten la profundidad. Nuestro cerebro, asegura Sugihara en una entrevista con lainformacion.com, tiende a interpretar los objetos como simétricos y esa forma de completar la realidad facilita el engaño.Pregunta. ¿Cuál es la historia detrás de estas ilusiones visuales? ¿Cómo empezó?Respuesta. Mi área de investigación es la ingeniería matemática. Y una de las líneas consiste en construir un ordenador que pueda interpretar dibujos lineales como objetos tridimensionales sólidos. Para comprobar cómo funciona, introducía imágenes de objetos imposibles en el programa, esperando que llegara a la conclusión de que esas imágenes eran incorrectas. Sin embargo, mi programa interpretaba a veces estos objetos como reales y así descubrí que algunos objetos imposibles no son realmente imposibles y pueden ser construidos como sólidos en tres dimensiones. A causa de esta experiencia empecé a interesarme por las ilusiones visuales, en particular por las de objetos en 3D en movimiento.P. ¿Qué es eso de la «Aproximación matemática a los objetos imposibles»?R. Una de las metas de mi investigación es construir un método matemático que permita a los ordenadores distinguir las estructuras en tres dimensiones y con profundidad de las imágenes en dos dimensiones. Y con esto puedo comparar la manera de percibir de los humanos con la de los ordenadores. Esta comparación da una nueva perspectiva de nuestros sistemas de percepción y las ilusiones visuales. Y esto es lo que yo llamo «aproximación matemática a las ilusiones visuales».P. ¿Cuáles son los principios por los que funciona la ilusión del tejado?R. Creo que nuestro sistema visual prefiere las estructuras simétricas a las no-simétricas a la hora de interpretar imágenes de objetos sólidos. En este sentido, el «tejado antigravedad» funciona de la misma manera que mi anterior ilusión, la de las «pendientes magnéticas». En este caso, nuestro cerebro interpreta que los dos aleros del tejado tienen la misma forma y en el otro caso interpretaba que los cuatro toboganes tenían la misma forma.P. Usted sostiene que nuestro sistema visual prefiere las formas rectangulares a las irregulares…R. Sí, la «rectangularidad» es un ejemplo típico de simetría. En el caso de la ilusión del tejado, la simetría surge al interpretar que el eje del tejado es perpendicular a la sección lateral. P. Sus trabajos recuerdan claramente los dibujos de M.C. Escher ,¿son su fuente de inspiración?R. Sí. Cuando empecé a utilizar mi programa informático para comprobar cómo interpretaba dibujos lineales, usé los dibujos de objetos imposibles como los que hacía Escher.P. ¿Es nuestro cerebro fácil de engañar? ¿Por qué?R. Porque las imágenes no contienen información sobre la profundidad y el cerebro debe adivinar, introduciendo información adicional como la rectangularidad o la simetría. Por otro lado, hay infinitas maneras de interpretar una imagen y sin este proceso no tendríamos manera de entenderlas.P. Con otras ilusiones comentó usted que los niños, cuyo sistema visual aún no ha sido modelado por la experiencia, raramente son engañados por estas ilusiones. ¿Sucede también aquí?R. Sí, eso sucede cuando les enseñamos imágenes fijas de objetos imposibles, como las escaleras de Escher. Los niños pequeños preguntan «¿qué tiene de divertido?». Pero cuando la imagen se mueve, como en estas ilusiones, hasta los niños entienden y se divierten con la magia del objeto imposible.* Si quieres construir tus propios objetos imposibles, Sugihara ofrece las plantillas necesarias en su página web.
¿Y si divido infinito entre infinito?
–Me encantan las luces de Navidad –exclamó Ven con los ojos llenos de reflejos de colores.
–Sí, son las noches más bonitas del año… –añadió Sal –Bueno, y las de verano cuando vemos en la playa las Perseidas.
–Es verdad, Sal –dijo el pequeño –, pero en Navidad las luces son de todos los colores.
–¿Por qué solo ponemos estas luces tan bonitas en Navidad, Mati? –preguntó el gafotas.
–Parece que su origen podría encontrarse en la época romana, en unas fiestas llamadas los Saturnales –les dijo –que eran muy populares porque en dichas fiestas los esclavos recibían más privilegios que en ninguna época del año. Como las fiestas coincidían con el final de los días más cortos del año, por el solsticio de invierno, lo entendían como el triunfo de la luz sobre la oscuridad y lo celebraban a la luz de velas y antorchas. Fue la popularidad de estas fiestas entre los romanos la que facilitó que los cristianos la asimilaran al nacimiento de su líder para que éstos, los romanos, pudieran convertirse a su religión sin renunciar a sus fiestas alrededor del solsticio.
–Pues sí que es el triunfo de la luz sobre la oscuridad –siguió Ven –, ¡han puesto infinitas luces este año!
–Hala, Ven –protestó Sal –, ya estás exagerando, no puede haber infinitas luces porque no hay infinitas calles y una calle no puede tener infinitas luces.
–Me estás liando… –se quejó Ven agachando su cabecita.
–Mira Ven, si hay un número finito de calles –continuó su hermano con cariño –, por ejemplo, 100 y hubiese infinitas luces en la ciudad, habría en cada calle infinito dividido entre 100 luces en cada calle, y si divides infinito entre un número sale infinito, ¿no?
–¿¿Sí?? –el pequeño abrió los ojos de para en par –¿Infinito dividido entre un número sale infinito?
–Eso es –confirmó Mati –, aunque realmente, infinito no es un número, es un concepto, pero si una cantidad crece mucho, acercándose al infinito, podemos decir que la división entre esa cantidad y un número fijo, se acerca también a infinito.
–No entiendo –confesó el pequeño Ven.
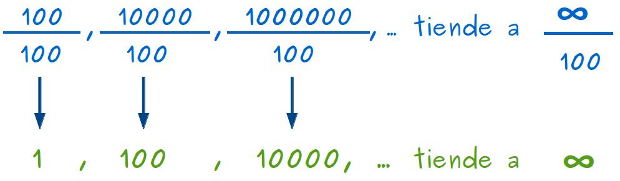
–A ver –dijo Mati –, pensemos en las siguientes divisiones: en el denominador siempre tenemos 100 y los numeradores van aumentando muy rápido, de forma que podemos decir que el numerador tiende a infinito y que , por lo tanto, estas divisiones se están a acercando a ∞ dividido por 100, ¿no?
–Vamos ahora a calcular el valor de esas divisiones –continuó Mati –. La primera sale 1, la segunda sale 100, la tercera sale 10000, y si siguiéramos aumentando el numerador, el resultado iría aumentando tendiendo a ∞:
–Claaaaro… –se asombró el gafotas.
–Por eso podemos decir, con muchas comillas, que ∞ dividido por un número es ∞ –les contó.
–¡Toma! –se alegró el pequeño.
–Ahora vamos a mirar estas divisiones en las que hemos hecho lo contrario –continuó la pelirroja –, hemos dejado fijos los numeradores y hemos ido aumentando los denominadores, para que sean ellos los que tiendan a infinito:
–¿Hacemos las cuentas, Mati? –preguntó el gafotas.
–Adelante, chicos.
–La primera da 1 otra vez –mascullaba Sal –, la segunda da 0,01… la tercera 0,001…
–Eso es, y si siguiésemos aumentando el denominador hasta el infinito, ¿qué pasaría? –les preguntó.
–Que nos saldría casi 0, ¿no, Mati?
–Eso es, Sal, muy bien.
–¡Eres el mejor! –dijo Ven a su hermanito.
–Los dos sois geniales –Mati guiñó un ojo –. Por esto, podemos decir, con muchas muchas comillas, que cualquier número dividido entre ∞ es igual a 0.
–¿Y si divido infinito entre infinito? –preguntó Sal.
–¡Pues 1! –gritó Ven asustando al pobre Gauss.
–Bueno, bueno… –dijo Mati misteriosa –. Vamos a investigar un poco, ¿queréis?
–¡¡Sí!! –gritaron los dos hermanitos.
–Si ponemos en el denominador ∞ y hacemos crecer los numeradores como en el primer ejemplo –les dijo Mati –, podríamos decir que esas divisiones tenderán a ∞ dividido por ∞, ¿no?
–Sí, sí, claro –dijo Ven muy serio.
–Pero al calcular el valor de las divisiones –continuó ella –, como un número dividido entre ∞ hemos dicho que vale 0, tenemos:
–O sea –dijo Ven –que ∞/∞ es igual que 0, ¿verdad, Mati?
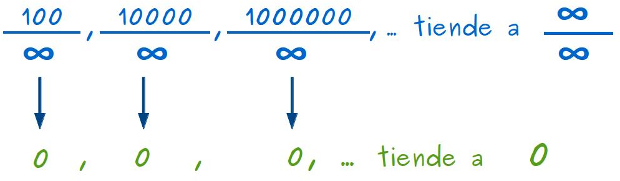
–O no… –respondió ella misteriosa –. Vamos a darle la vuelta a a las divisiones, en el numerador ∞ y el denominador creciendo muy rápido:
–¿Qué pasa al calcular el valor de estas divisiones? –les preguntó.
–Infinito dividido por un número es infinito… –decía Sal –. Todas dan como resultado infinito.
–Ajá –confirmó Mati.
–¡Ahí va! –se extrañó Ven –Ahora resulta que ∞/∞ también puede ser infinito…
–¿Cómo sabemos si ∞/∞ es 0 o es infinito?
–U otra cosa, ¿no? –dejó caer Mati misteriosa.
–¿¿Otra cosa?? –exclamó Ven –¡¡Imposible!!
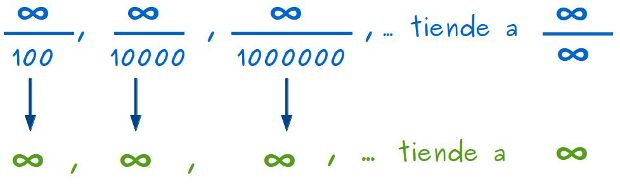
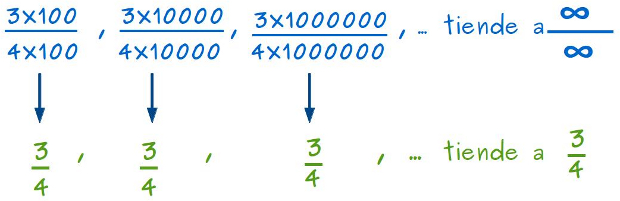
–Fijaos en las siguientes divisiones –les propuso –, ahora hacemos crecer mucho tanto el denominador como el numerador… por lo tanto, también crecerían hasta ∞/∞, ¿no?
–¡Toma, claro! –dijo Ven muy afectado.
–Pues, calculad ahora el valor de las divisiones –les retó —, a ver qué pasa…
–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven de pronto –¡Ahora resulta que ∞/∞ es igual que 3/4!
–Entonces, Mati –preguntó Sal —Si te preguntan cuánto es ∞/∞, ¿qué responderías?
–Que no lo sé, que depende… que es un valor indeterminado, que depende cómo se acerquen al infinito el numerador y el denominador… –les dijo –Es hermoso no saber cómo va a terminar todo en esta vida, ¿no creéis?
–Pues… –dudó Ven y añadió –Sí, es hermoso, a mí me gustan las sorpresas.